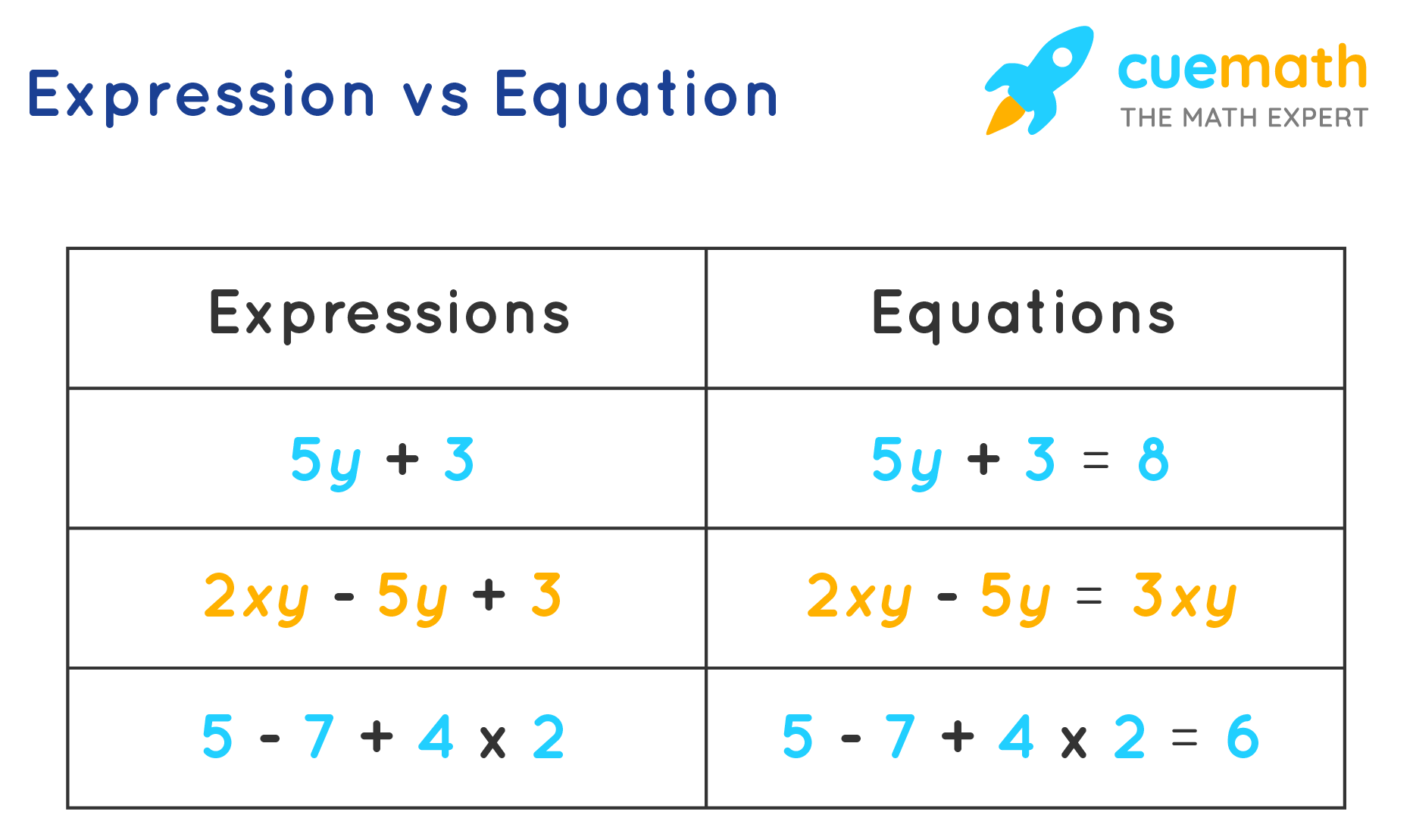
Algebra is a branch of mathematics that deals with symbols and the rules for manipulating those symbols. In algebra, terms are the building blocks of equations and expressions. Understanding different types of terms is crucial in solving algebraic problems. Let’s explore some examples of terms in algebra.
Terms in algebra can be constants, variables, coefficients, or a combination of these elements. Each term has a specific role in an equation or expression, and knowing how to identify and work with these terms is essential for success in algebra.
Examples of Terms in Algebra
One common type of term in algebra is a constant. A constant is a specific value that does not change, such as 3, -5, or 1/2. Constants are standalone terms that can be added, subtracted, multiplied, or divided in equations and expressions.
Variables are another important type of term in algebra. Variables, such as x, y, or z, represent unknown quantities that can vary. These terms are placeholders for numbers that can be determined through solving equations or expressions.
Coefficients are the numbers that are multiplied by variables in algebraic terms. For example, in the term 3x, the coefficient is 3. Coefficients can be positive, negative, fractions, or decimals, and they play a crucial role in manipulating algebraic expressions.
Terms in algebra can also be a combination of constants, variables, and coefficients. For instance, in the term 2x + 5, there are two terms: 2x and 5. The term 2x consists of the coefficient 2 and the variable x, while the term 5 is a constant.
Another example of a term in algebra is a binomial, which consists of two terms connected by a mathematical operation. For instance, in the expression 2x + 3y, there are two terms: 2x and 3y. Binomials are common in algebraic equations and are essential in solving algebraic problems.
In conclusion, terms in algebra are the fundamental elements of equations and expressions. By understanding the different types of terms, such as constants, variables, coefficients, and binomials, students can effectively solve algebraic problems and equations. Practicing with various examples of terms in algebra is key to mastering this branch of mathematics.